Los números armónicos se conocen desde la antigüedad y se definen como la suma de los recíprocos de los primeros n números naturales: \(H_n = 1+ \dfrac 1 2 + \dfrac 1 3 + ...+ \dfrac 1 n \).
Por ejemplo
\(H_{10}= 1 +\dfrac 1 2+\dfrac 1 3 +...+\dfrac 1 {10} =2.9289682539682538\)
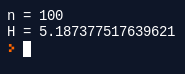
Y así con cualquier valor de n
El recíproco de un número x es \( \dfrac 1 x \)
Crea un programa que pida qué número armónico se desea, calcule el número armónico y muestre el resultado.
Ejemplo de la salida del programa
Pulsa el botón Pseudocódigo para obtener una descripción detallada de lo que hay que hacer.
Definir la función armonico(n)
Asignar el valor 0 a la variable H
Bucle for desde x = 1 hasta n
Sumamos H con el recíproco de x y asignamos el resultado a H
Devolvemos el valor de H (fin de la función)
Resto del programa:
Pedimos al usuario el valor de n que deseamos calcular
Llamamos a la función armonico(n) pasándole el valor de n y guardamos el resultado devuelto en una variable
Imprimimos por pantalla el valor del número armónico devuelto anteriormente por la función.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0